Comment calculer le périmètre d’un cercle

Le calcul du périmètre d’un cercle est classé parmi les fondamentaux en géométrie enseigné dans établissement scolaires. Assez pratique pour résoudre certains problèmes non seulement pendant le cursus scolaire, mais aussi dans la vie courante. Comment procéder pour calculer le périmètre d’un cercle ? Cet article vous explique comment procéder pour calculer le périmètre dun cercle.

Qu’est ce qu’un cercle ?

Avant de vous initier aux formules de calcul du périmètre d’un cercle, il est important de retourner aux notions de base. En général, le terme cercle est souvent confondu avec les termes tels que rond, disque ou sphère.

A découvrir également : Comment activer TV Orange Sosh ?

Un cercle est défini par une courbe fermée constituée de points situés à distance égale d’un autre point (centre). La distance entre le centre et les différents points est appelée rayon du cercle. Le diamètre, c’est un segment de droite allant d’un point du cercle vers un autre en passant par le centre. Le diamètre du cercle représente le double de la longueur du rayon du cercle.

Première méthode de calcul du périmètre d’un cercle

Pour ce qui est du calcul proprement dit du périmètre du cercle, une formule standard est souvent utilisée. Il s’agit de la formule ci-après : Périmètre du cercle = rayon x 2 x π

A lire également : Stockage en ligne : les points forts et les limites à connaître

En observant la formule de calcul du périmètre du cercle, vous retrouver le nombre π, disponible sur toutes les calculatrices scientifiques. Vous devez sans doute savoir que π est nombre décimal qui n’a pas de fin. Cependant, vous pouvez le réduire tout simplement à 3,14 pour simplifier les calculs.

Un exemple serait idéal pour appliquer la formule donnée précédemment pour davantage de compréhension.

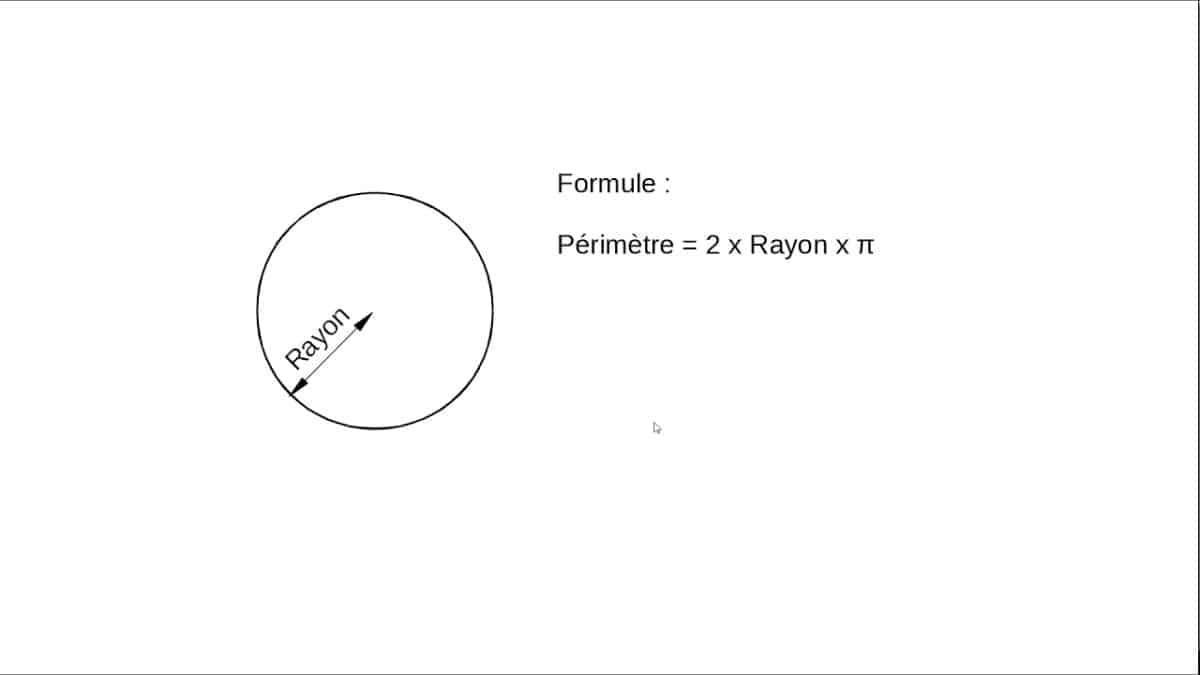Exemple :

On vous présente un cercle dont le rayon r mesure 6cm. Quel sera le périmètre du cercle dans ce cas ?

Tout d’abord vous posez la formule : Périmètre du cercle = rayon x 2 x π.

Ensuite vous appliquez avec les données que vous avez 6 x 2 x π avec π égal à 3.14 ce qui donne un résultat de 37,7. Ainsi, le périmètre de votre cercle ici serait égal à 37,7 cm.

Aussi vous avez la possibilité de calculer le demi-périmètre dun cercle. Dans ce cas, il vous suffira de poser la formule r x π tout court.

Deuxième méthode de calcul du périmètre d’un cercle

En outre, lorsqu’on pousse l’analogie entre le rayon et le diamètre, une deuxième formule de calcul se présente. Vous savez déjà que le diamètre fait 2 fois la longueur du rayon d’un cercle. Du coup, on peut également déterminer le périmètre de la même façon. La formule standard du périmètre du cercle est : Périmètre du cercle = rayon x 2 x π, dans le présent la formule serait = diamètre x π.

Vérifions la fiabilité de cette formule avec un exemple. Toujours avec un cercle dont le rayon est de 6 cm, on en déduit que le diamètre est de 12 cm.

Dans ce cas, vous posez la deuxième formule : Périmètre = diamètre x π. Ensuite vous posez périmètre égal 12 x 3,14 = 37,7 cm. Vous constaterez que le périmètre obtenu est identique à celui obtenu à partir de la formule standard.

En somme, voilà comment procéder pour déterminer le périmètre dun cercle.

Les unités de mesure du périmètre d’un cercle

Maintenant que vous savez comment calculer le périmètre d’un cercle, il est temps de se pencher sur les unités de mesure utilisées pour exprimer cette grandeur. Le périmètre d’un cercle peut être mesuré en centimètres, mètres ou kilomètres.

En général, on utilise le centimètre (cm) pour les petits cercles tels que ceux qui apparaissent dans des dessins techniques ou graphiques. Les circonférences plus grandes sont généralement mesurées en mètres (m). Lorsque l’on traite avec des propriétés terrestres telles que la distance entre deux villes par exemple, le kilomètre est souvent utilisé.

Comment convertir une unité à une autre ? Rien de plus simple ! Il suffit de connaître les facteurs de conversion correspondants : un kilomètre (km) = 1000 mètres (m) et un mètre (m) = 100 centimètres (cm).

Prenons un exemple concret : imaginons qu’on a besoin de calculer la longueur du mur circulaire autour d’une piscine dont le rayon mesure 6 mètres. La formule standard nous donnerait comme résultat Périmètre = rayon x 2π soit Périmètre = 6 x 2 x 3,14 = 37,68 mètres.

Si on voulait maintenant exprimer ce résultat en centimètres plutôt qu’en mètres mais sans refaire tous les calculs depuis le début, il suffirait donc tout simplement de multiplier notre valeur initiale (37,68) par 100 afin d’obtenir sa version équivalente en cm : Périmètre = 37,68 x 100 = 3768 cm.

Il faut bien comprendre quelles unités sont les plus adaptées à chaque situation, et être capable de passer facilement de l’une à l’autre en utilisant les bons facteurs de conversion.

Applications pratiques du calcul du périmètre d’un cercle

Maintenant que vous êtes un expert dans le calcul du périmètre d’un cercle, il est temps de découvrir les applications pratiques de cette grandeur. Effectivement, connaître la circonférence d’un cercle peut être très utile dans des domaines tels que l’ingénierie, la construction ou encore l’architecture.

Par exemple, si vous envisagez de construire une clôture circulaire autour de votre jardin et que vous connaissez le rayon souhaité pour ce dernier, alors vous pouvez utiliser notre formule standard : Périmètre = rayon x 2π pour déterminer précisément la quantité exacte de matériaux dont vous aurez besoin pour cet aménagement paysager.

De même, si vous travaillez sur un projet architectural qui nécessite des colonnes circulaires auxquelles viennent s’articuler différentes poutrelles à 360°, tel qu’une place publique par exemple, grâce au calcul du périmètre d’un cercle, il sera plus facile d’estimer correctement les dimensions requises pour ces éléments architecturaux ainsi que de prévoir leur forme exacte.

Dans le domaine industriel, dans certains cas où une tuyauterie doit être installée sur un périmètre circulaire, en utilisant notre formule standard : Périmètre = diamètre x π, on peut déterminer avec précision la longueur totale nécessaire à cette installation. Il existe aussi d’autres exemples où la connaissance du périmètre d’un cercle peut être utile, telle que le dimensionnement d’une roue pour un véhicule. De manière générale, la capacité de calculer avec précision et rapidité la circonférence d’un cercle peut être un atout précieux dans de nombreuses professions.

En outre, la formule standard pour calculer le périmètre d’un cercle est simple et facile à utiliser. Elle peut aider dans divers domaines tels que l’architecture, l’ingénierie ou encore l’aménagement paysager. Il faut connaître les unités de mesure adéquates pour exprimer cette grandeur afin d’être en mesure de passer facilement de l’une à une autre grâce aux facteurs de conversion correspondants.